Hello, there!

I'm very excited to announce that my latest paper has been accepted for the SIGMOD 2022 conference! It is my most ambitious work so far, and now that the peer-review process is over, I can finally disclose some details about it.

My work consists in a novel explainability framework for embedding-based Link Prediction models, named Kelpie. Given any link yielded by an embedding-based model, Kelpie can identify why the model predicted it by extracting various types of explanations.

By the way, Kelpies are mythological shapeshifting fish-horse creatures said to dwell in the depths of Scottish lakes, so they seemed the perfect mascot for a machine learning / deep learning project *ba-dum tsss*. Also, “Kelpie” makes a nice acronym: “Knowledge graph Embeddings for Link Prediction: Interpretable Explanations”.

Since this work is heavily invested in Link Prediction on Knowledge Graphs, allow me to start with a brief recap on the topic 😁

Knowledge Graphs and Link Prediction

As I already mentioned in the past, Knowledge Graphs are repositories of real-world information where entities are connected via edges labeled by relations: they thus form <head, relation, tail> triples called facts. Knowledge Graphs are powerful but generally incomplete; Link Prediction tackles this issue by inferring new facts from the patterns and semantics of the already known ones.

Most Link Prediction models nowadays map the entities and relations in the graph to vectorized representations called Knowledge Graph Embeddings. Embedding-based Link Prediction models generally define a scoring function Φ that, given a head entity, a relation, and a tail entity, uses their embeddings to estimate a plausibility value for the corresponding fact. The embeddings of all entities and relations are usually initialized randomly, and then trained with Machine Learning methods to optimize the Φ values of a set of facts known to be true a priori (i.e., our training set). The trained embeddings should generalize and result in high plausibility scores for unseen true facts too.

Explainability and Link Prediction

Embedding-based models have achieved promising results in Link Prediction, often surpassing traditional rule-based counterparts. Unfortunately, these systems are almost always opaque: the embedding of an entity or relation is just a vector of numbers, with no memory of which training facts have been most influential to it, and with no insights on why it supports certain predictions while hindering others.

Explaining the outcomes of embedding-based Link Prediction models is thus becoming an increasingly urgent challenge. Link Prediction models are often used in scenarios that inherently require explainability, such as fact checking or drug discovery and repurposing; furthermore, explanations can reveal if our systems are leveraging reliable patterns or rather spurious correlation, thus assessing their trustworthiness (or lack thereof).

One could ask: “Why don’t we just use one of the general-purpose explainability frameworks that are already out there? Why do we need a new framework specific for Link Prediction?” The answer is that, unfortunately, no general-purpose frameworks seem to apply well to embedding-based Link Prediction models.

Most explainability frameworks operate by perturbing the features of the input samples and then checking the resulting effect on predictions: if the prediction outcome changes, it means that the perturbed features were relevant, or salient, to it. These saliency-based frameworks, unfortunately, are only useful when the input features of samples are directly interpretable by humans: e.g., macro-pixels in images, or words in a sentence. In the case of Link Prediction, samples are just triplets of embeddings: perturbation approaches would thus just identify the most salient components of those vectors, which would not be informative from a human point of view.

A few frameworks follow a different paradigm, and try to identify the training samples that have been most influential to the prediction to explain. The approach by Koh and Liang, based on the robust statistics concept of Influence Functions, is considered the cornerstone of this category. This approach seems quite sensible for our scenario; unfortunately, Influence Functions are computationally very expensive, and this approach has been proved unfeasible to explain Link Predictions.

Introducing Kelpie

Kelpie overcomes these issues by mixing the advantages of both categories of frameworks. On the one hand, similarly to Influence Function methods, Kelpie explains predictions in terms of the training samples that have enabled them in the first place: on the other hand, it identifies those training samples with a custom, saliency-inspired approach which is feasible for the Link Prediction field.

More specifically, Kelpie interprets any tail prediction <h, r, t> by identifying the enabling training facts mentioning the head entity h, and, analogously, any head prediction by identifying the enabling facts featuring the tail. Given any tail prediction <h, r, t>, Kelpie supports two different explanation types:

• a necessary explanation is the smallest set of training facts mentioning h such that, if those facts are erased from the training set, the model (retraining it from scratch) will predict a different tail for head h and relation r.
  

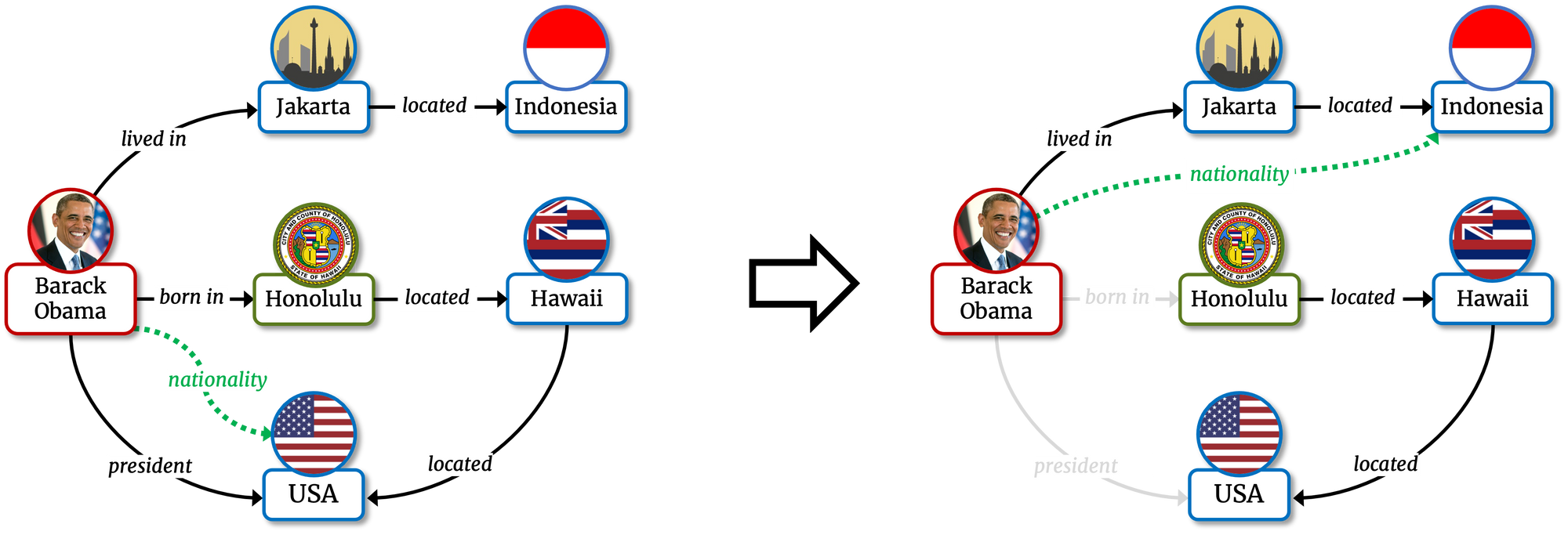
Given the tail prediction <Barack Obama, nationality, USA>, a necessary explanation is the set {<Barack Obama, born_in, Honolulu>, <Barack Obama, president, USA>} if, removing those facts from the training set, the model ceases to predict that Barack Obama is American.

• a sufficient explanation is the smallest set of training facts mentioning h such that, if those facts are added to any random entity e, the model (retraining it from scratch) will predict <e, r, t> too.

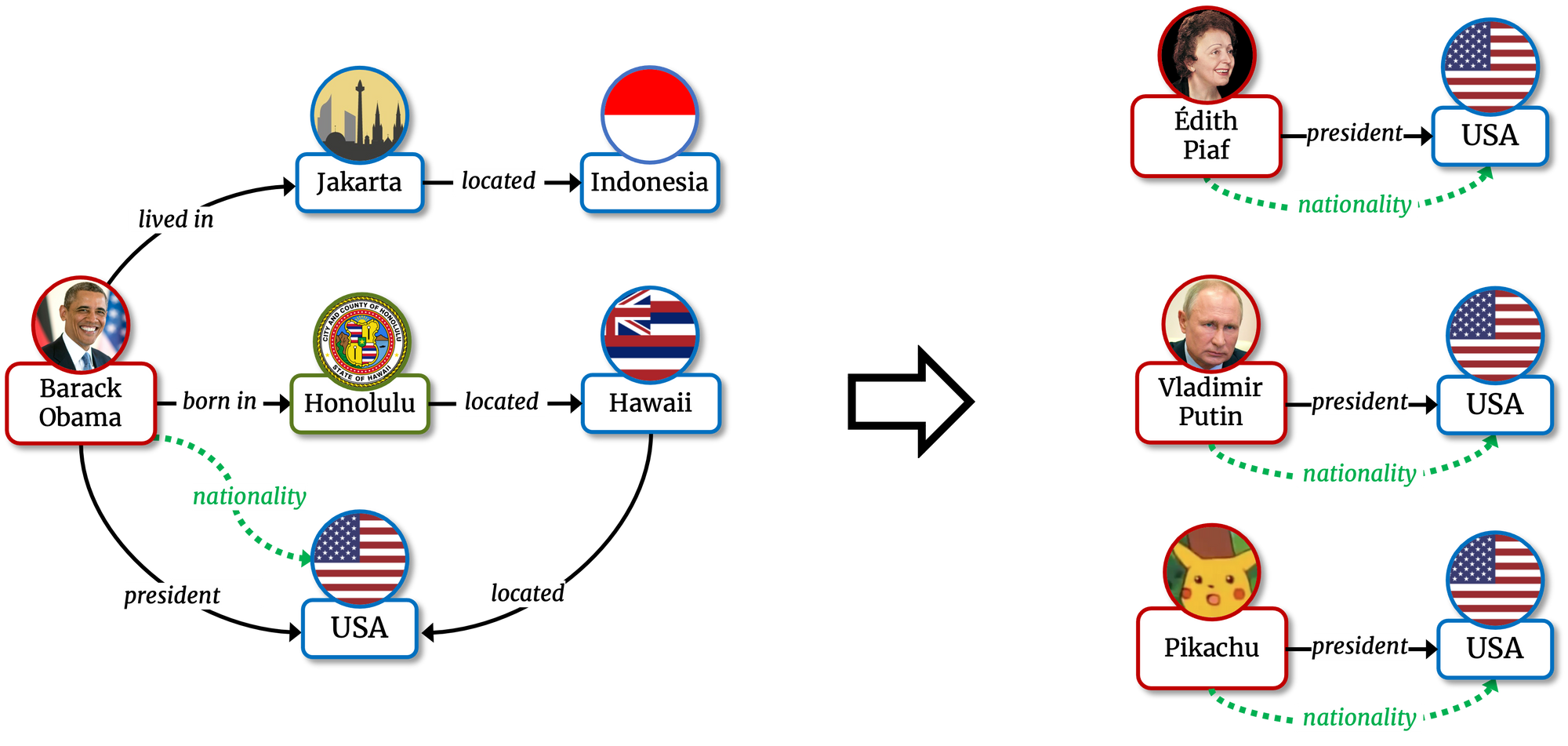
Given the tail prediction <Barack Obama, nationality, USA>, a sufficient explanation is the fact <Barack_Obama, president, USA> if, adding the USA presidency to any non-American entity (e.g., Édith Piaf, Vladimir Putin, or Pikachu) the model starts to predict their nationality as USA.

The same concepts apply to head predictions as well.

In order to identify which sets of facts constitute necessary or sufficient explanations, Kelpie creates alternate versions of the already existing entities, called mimics. A mimic is featured in the same training facts as the original entity it refers to, except for a few purposefully injected perturbations, i.e. removals or additions. Ideally, a mimic should display the same behavior that the original entity would have shown if its training facts had been perturbed in that way since the very beginning. By creating mimics and checking how their predictions differ from those of the original entities, we are able to verify which sets of facts constitute a necessary or a sufficient explanation to the prediction to interpret.

Clearly, mimics are only useful as long as they are both faithful to the behavior that the embeddings of original entities would have displayed, and feasible in the way they are computed. For example, a faithful mimic can be easily obtained by actually re-training the model from scratch after injecting the perturbations; the heavy computational costs of re-training the whole model, however, would make this approach unfeasible.

Kelpie generates mimics that are both faithful and feasible by relying on a novel Machine Learning methodology that we have called post-training. The embedding of any mimic is initialized randomly, as any other entity embedding; then, it undergoes a training process analogous to the original training in terms of optimizer and hyper-parameters, but with two key differences:

• Except for the embedding of the mimic, all the other embeddings and shared parameters are kept frozen and constant: the only component that gets updated in the training process is the embedding of the mimic.
• Since the embedding of the mimic is the only one that gets updated, the training set is limited to the training facts that actually feature the mimic entity, i.e., to the perturbed set of training facts of the original entity.

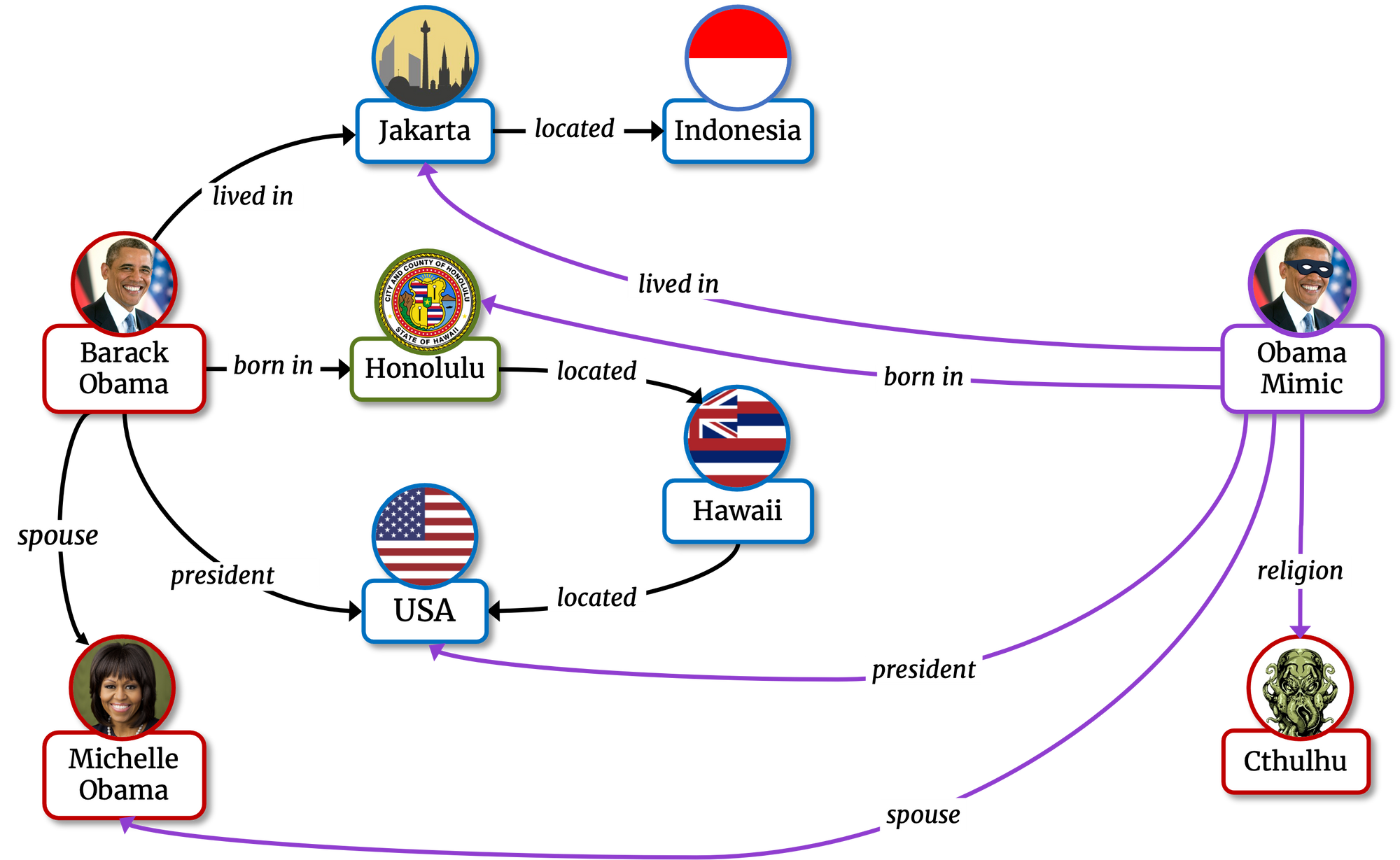
The Obama Mimic is an alternate version of Barack Obama: its facts (in purple) are identical
to those of the original Barack Obama, except for a few injected perturbations.
And, yeah, in an alternate universe Barack Obama is a Cthulhu cultist.

These differences make the post-training a very lightweight process, because it only involves one embedding (instead of thousands) and it only optimizes the scores of a few dozens or hundreds of facts (instead of hundreds of thousands). In practice, while fully training a Link Prediction model usually takes several hours, a post-training process is generally over in a few seconds. This makes it possible to use post-training to discover which perturbations would affect the prediction to explain the most, and, thus, which training facts enabled it.

Finally, an aspect I am particularly proud of is that, thanks to the flexibility of post-training, Kelpie can theoretically support any Link Prediction models based on embeddings: this is a sorely needed quality in a field where dozens of new models are released each year.

That’s it for this post!

As usual, I will leave here some references to additional contents:

• you can find here the papers of three general purpose explainability frameworks: LIME, ANCHOR, and SHAP. They all have had a big impact in the AI community.
• here are the links to Data Poisoning and CRIAGE, two very interesting data poisoning frameworks for Link Prediction models. Rather than explaining predictions, they focus on verifying the robustness of the learned embeddings to perturbations. Since their techniques and experiments partially overlap with ours, we have used them in our Kelpie as a baseline.

See you next time! 👋