Using Embeddings to Predict New Links in Knowledge Graphs

Hello, there!

This is my very first post, so I'm super excited. I'd like to talk about my current field of research, which deals with how Machine Learning techniques can be applied to Link Prediction on Knowledge Graphs.

Knowledge Graphs are stores of real-world information structured into nodes and labeled directed edges. Nodes represent entities (people, places, etc) and they are connected by edges whose labels convey semantic relations.
In a Knowledge Graph an edge linking two nodes represents a unit of information called fact, i.e., <Barack_Obama, was_born_in, Honolulu>.

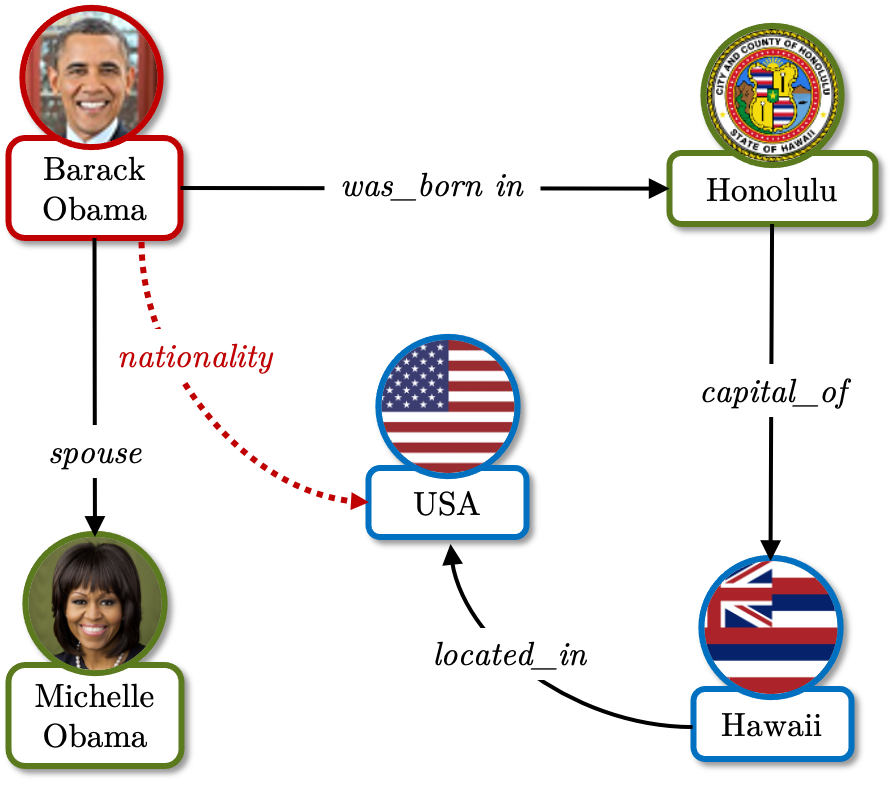
A wee little Knowledge Graph.

Knowledge Graphs are quite useful and they are employed in a wide variety of contexts, from semantic web projects to user profiling and recommendation systems. Unfortunately though, all Knowledge Graphs tend to suffer from incompleteness, as they only contain a small portion of all the real-world information they should encompass.

Link Prediction tackles incompleteness by inferring new facts from the existing ones. For instance, knowing that <Barack_Obama, was_born_in, Honolulu> you can deduce that, probably, <Barack_Obama, has_nationality, USA> (assuming it was previously unknown).

Nowadays, most Link Prediction models map each entity and relation to vectorized representations called embeddings. Link Prediction model based on embeddings usually works by defining a mathematical scoring function Φ that, for any fact <h, r, t>, can use the embeddings of h, r, and t to compute a floating point output value Φ(h, r, t) .

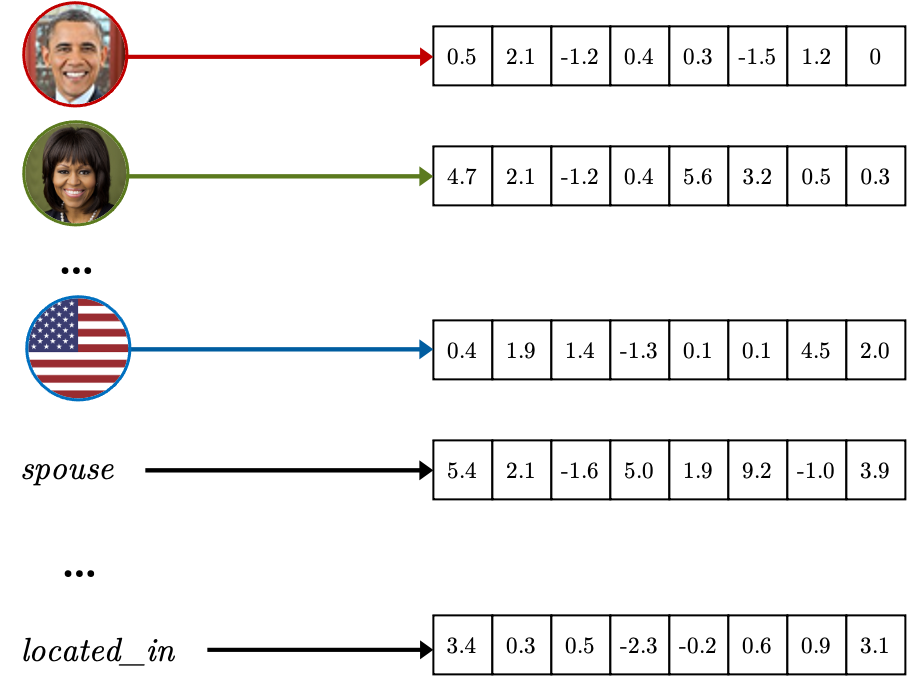
Each entity and relation is mapped to an embedding.

In training, all the embeddings are initialized randomly, and then optimized to maximize the scores Φ of the known facts. In other words, we tweak and improve the values for the embeddings of all entities and all relations so that, for any known fact <h, r, t>, we make Φ(h, r, t) become as large as possible. In practice, what we actually gather the Φ scores of all the known facts in a Loss Function (e.g., Negative Log-Likelihood, Binary Cross-Entropy, or Pairwise Ranking Loss), and train the embeddings to optimize the Loss value.

After the training is complete, the learned embeddings should (hopefully!) be able to generalize and to lead to high Φ values even for true facts that were not seen in training. So we can discover new relevant facts by just trying new combinations <entity_1, relation, entity_2> and their Φ score: if it is good enough, chances are the combination corresponds to a true, previously unknown, fact. In other words, after we have carefully trained the embeddings, we expect Φ to be a good estimate of the plausibility of any (known or unknown) fact.

Does this seem a bit too convenient? Well, it should 😜 In practice, the hardest part of building a new Link Prediction model is devising a "good" Φ  function. Many functions sounded very good at first, but in time unexpected flaws emerged.

At this regard, the TransE model is a fine example. TransE was created by Bordes et al. in 2013; it is a pioneering work, and one of the very first Link Prediction models based on embeddings in history. TransE was largely inspired by the translational properties Word2Vec neural language model, and it enforces the translational operation explicitly in its scoring function Φ:

Φ(h, r, t) = |h + r - t|

The scoring function of TransE can be read in this way: given the fact <h, r, t> we take into account the vector of the head entity h and we translate it by the relation embedding r; if the fact was true, we expect to land on a position close to the embedding of t (distance is measured with L1 or L2 norm). In a space with 3-dimensional embeddings, applying the Φ  function of TransE would look like this:

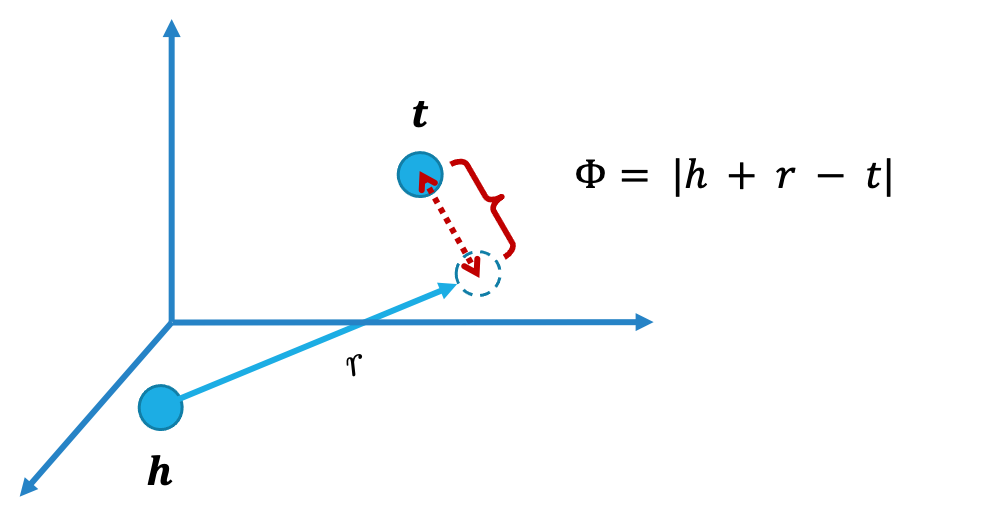
TransE scoring function in a nutshell.

This is a very simple Φ  function inspired by basic geometry, but for many cases it works pretty well. For instance, it was found to correctly predict the Capital cities of various countries:

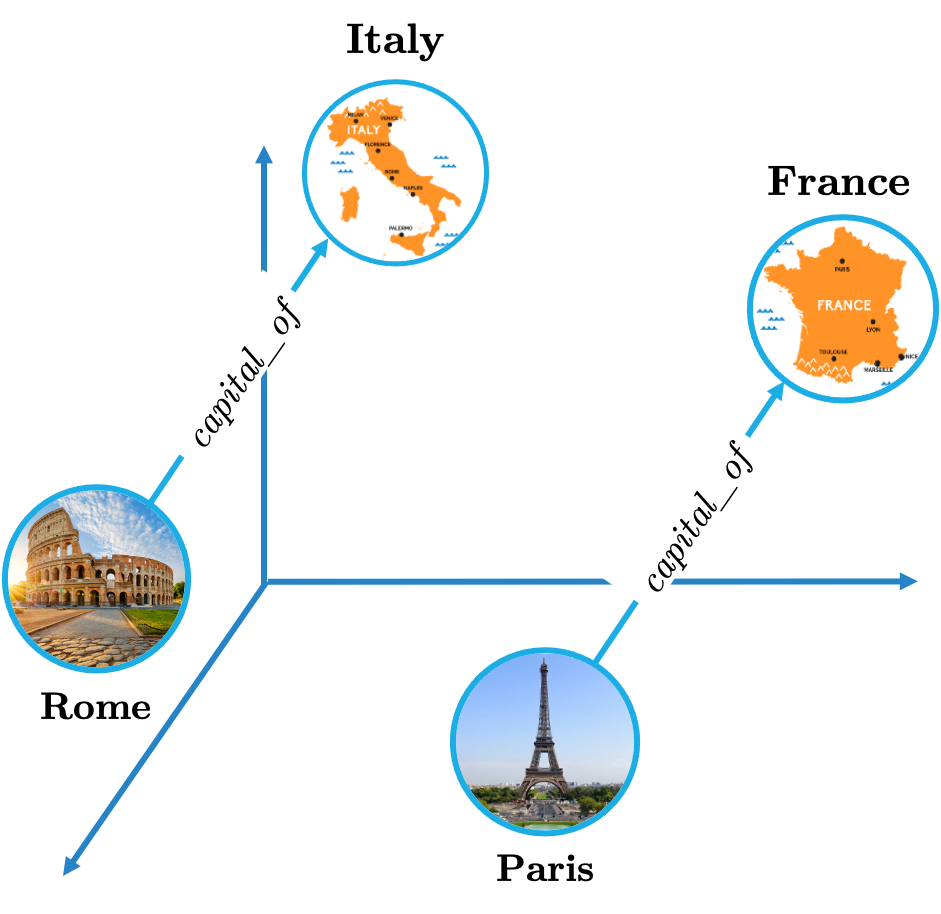
TransE is good on one-to-one relations, such as capital_of.

Unfortunately for TransE, though, not all relations are as smooth as capital_of.
Many relations may convey “one-to-many” semantics: the same head entity can be connected by the same relation to multiple tail entities, e.g.,  the same uncle can have multiple nephews: <Donald, uncle_of, Huey>, <Donald, uncle_of, Dewey>, and <Donald, uncle_of, Louie>.

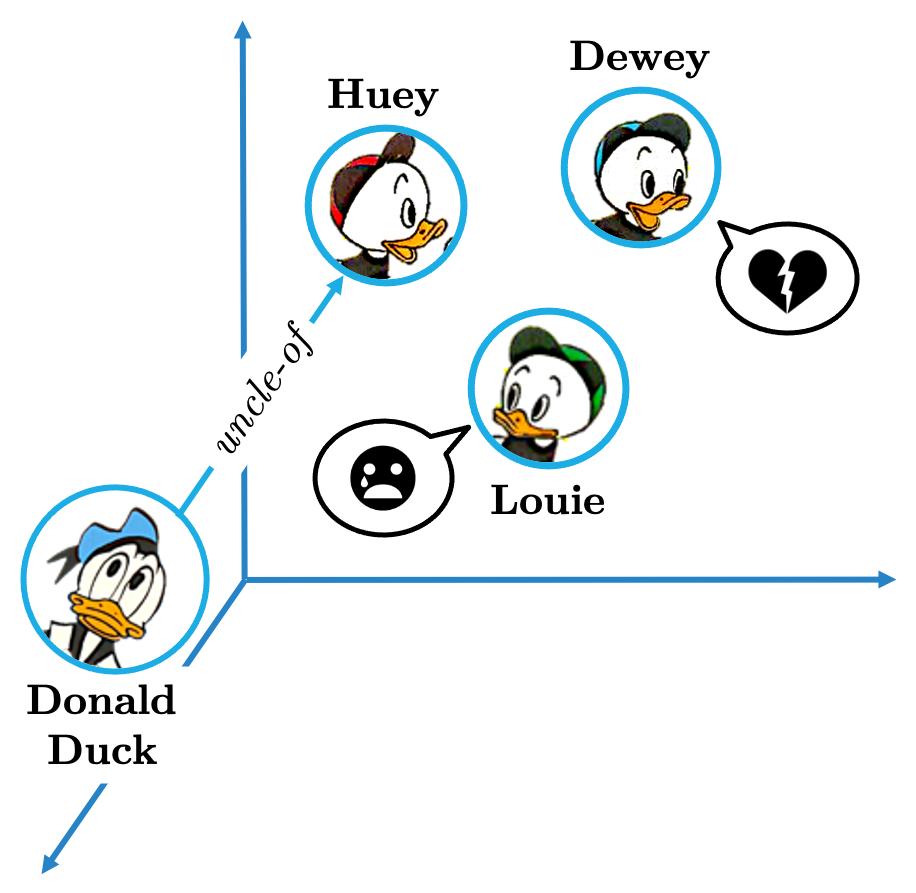
"You are a terrible uncle, unca' Donald!"

In cases like this, TransE fails spectacularly. Starting from the same head entity (e.g., Donald) and applying the same relation translation (e.g., uncle_of), we will just land in one spot of the vector space; and a single spot is not likely to lead equally good Φ values for all the correct tail entities (Huey, Dewey and Louie). The same issues occurs with many other types of relations: for starters, many-to-one and many-to-many relations, but also symmetric relations, transitive relations, and so on.

After this flaw was found, researchers did what they do best: they developed new models trying to overcome this issue, and then the next one, and so on. In time, new families of Φ functions have been tailored, each with its own pros and cons. Starting from TransE, in just a few years Knowledge Graph embeddings have become a sparkling research topic, with dozens of new models being proposed every year.

I don't want to get into too much detail - I will probably cover this in another post - but often times the Φ  function of such models also includes the use of deep machine learning architectures, such as convolutional or recurrent layers.
The weights of such layers can be seen as just additional parameters that are learned at the same time as the embeddings of entities and relations. Since they do not refer to any of the KG entities or relations, but rather affect all of them, in the Link Prediction field they  are often called “shared parameters”.

Thank you for reading this far! Of course this is just an overview, and there are a lot of details worth exploring… but that’s a topic for another day 😄

I will just leave here some material further materials if you are curious to delve deeper into these topics:

• First of all, here is the original TransE paper published in the NIPS conference in 2013. I will also leave here a link to the Word2Vec paper inspiring it;
• I would also like to reference this extensive comparative analysis among Link Prediction models published in the TKDD Journal. I have written it myself, so I'm quite proud of it!

That’s it! Have a nice day 👋